Out of all the Greeks in options trading, Rho is capable of providing uniquely critical insights that others cannot offer. Rho measures an option contract’s susceptibility to changing interest rates.

We’ll explain how Rho by defining its specific functions, how interest rates impact options trading, and cover some pertinent scenarios.

What is Rho in Options Trading?

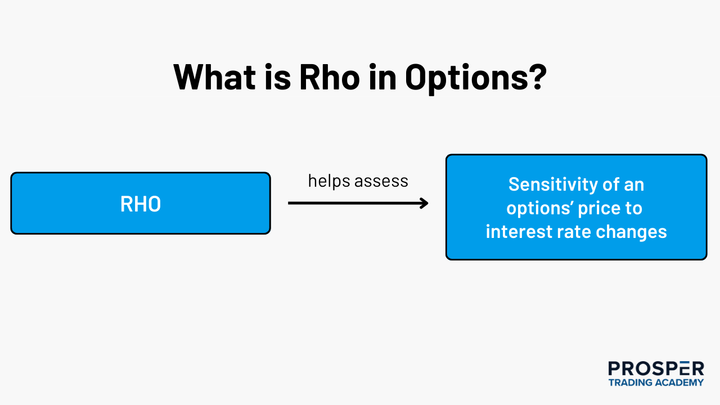
In layman’s terms, Rho calculates the sensitivity of an option contract to changes in interest rates. Options traders can use Rho to understand how changing interest rates may potentially affect the value of their positions. It signifies the monetary amount an option will change, relative to one percent point in interest rates.

For example: Let’s say an option contract has a Rho of $0.50. That’s how much it will increase or decrease for every one percentage point interest rates rise or fall.

Rho can also be used in this context not just for a single option contract – but an entire option portfolio. It’s also capable of measuring the cumulative risk exposure multiple options positions might have to changing interest rates.

The most sensitive options contracts to interest rates are typically at-the-money, are tied to high-priced underlying stocks, and have longer-term expiration dates. This is because the effects interest rates have on them are applicable to factors like cost over time. The effects higher interest rates have on options contracts that meet these requirements typically result in higher absolute Rho values.

Understanding Interest Rates

Interest rate values are measured in units called basis points (bps) – where 100 bps equals one percentage point. Under normal circumstances, interest rates move at a gradual pace – typically around .25% (25 bps) per quarter, so about 1% (100 bps) per year on average.

When the Fed makes their announcements on interest rates, they’re essentially referring to ones that are paid on US Treasury bills. These typically entail loans the Federal Reserve gives to monetary institutions – like banks and credit unions. They’re are issued overnight, and on an uncollateralized basis. Naturally, any changes the Fed might impose have a trickle-down effect on businesses, individuals, and other entities who take loans from these institutions – hence, why news centered around changing interest rates have such widespread effects on the economy.

To reiterate, interest rates can affect the cost of holding an option contract over time – especially when taking the cost of capital into consideration. Despite their impacts, the risks presented by interest rates are rarely factored into many modern options trading tools. From the Great Financial Crisis back in 2008-09, until the Fed started hiking rates a couple years ago, Rho was the forgotten “Greek.” Since rates were near zero, there was relatively little impact on the price of an option.

When applying Rho in options trading, it’s most ideal in scenarios when the Fed is regularly changing interest rates by at least 100 bps. Rho would have been especially useful during the rate hikes we saw in 2022. Moreover, this metric could arguably play a vital role if – and when – rates eventually start to fall.

Defining Positive & Negative Rho in Options Trading

Rho is measured in decimal units of one hundredth (.01, .02, .03, etc.) with positive and negative values. In most cases, positive and negative Rho are respectively used for specific types of options trades.

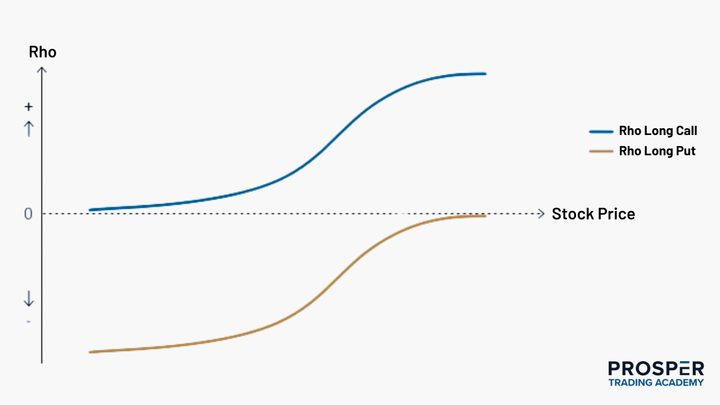
Positive Rho applies to long calls and short puts.

Negative Rho is for long puts and short calls.

Positive Rho

Rho is positive for long calls and short puts. Long calls give you the right to buy an option contract’s underlying stock. Short puts, have an obligation to buy an option contract’s underlying stock. Since both of these options contracts are betting on a stock price to rise, we’ll refer to long calls in this explanation, as the same principles essentially apply.

Long calls increase as the underlying stock price rises. Rho is positive for purchased calls as higher interest rates increase premiums for call contracts. As a result, the cost of that right is typically less than a call contract’s fully exercisable value (the intrinsic value of an option if it were exercised at the underlying stock’s current market price). The difference in cost between a call contract’s right to purchase and its fully exercisable value can be deposited into an interest-bearing account, making them more ideal for options traders in high-interest environments.

For example: Let’s say the value of a stock you buy has a market price of $50. The total cost of 100 shares for that stock is $5,000. If you buy one option call for that $50 stock at a $10 premium, the cost to control those 100 shares is $1,000.

The fully exercisable value for those shares in this example is $5,000. That means the cost of buying a call option for it requires significantly less upfront capital. The $4,000 difference is what could be deposited in an interest-bearing account. That balance would be positively reflected in the value of long call options when interest rates rise.

Negative Rho

Negative Rho generally applies long puts and short calls. For context, long puts give you the right to sell. Short calls also bet on the underlying stock price to fall, but have an obligation to sell. Since both of these options contracts are banking on the underlying stock price to fall, we’ll use long puts as our term of reference.

Rho is negative for purchased puts as contract premiums decrease due to higher interest rates. Since long puts give you the right to sell shares at a predetermined price, the capital used results in debit (ie, cash used to pay for the option contract). When shorting a stock, however, the capital received from this sale can still be deposited into an interest-bearing account. This is why long puts aren’t necessarily ideal for options traders in high-interest rate environments.

For example: Shorting stock value – Sell 100 shares of Stock XYZ at $500 per Share = $50,000 Total Proceeds ($500 x 100 Shares)

Buying Put Option – Buy 1 $500 Put at $750 Premium = $750

The total exercisable value for this option is $50,000 (the right to sell 100 shares at $500).

The cost to purchase the option ($750) is more upfront capital than the proceeds the total exercisable value would generate in an interest-bearing account.

The $50,000 from the short sale could be deposited and earn interest. This is why Rho negatively affects the value of a long put option as interest rates change.

Conclusion

Since interest rates are rarely factored into modern options trading tools, Rho can give traders a huge potential edge. This Greek offers unique insights on how pricing for an options contract can be affected by changing interest rates. It can be a vital metric that helps traders navigate volatile market conditions with high – or fluctuating – interest rates.

With interest rates expected to start coming down in the near term, Rho can potentially improve a trader’s ability to manage their portfolio’s options contracts. It can also help them identify additional high-profit potential options trading opportunities as interest rates change. It’s always important to do thorough research, and weigh your risk tolerance in any trade you consider making – which underscores the critical role Greeks like Rho can play when making these trading decisions.